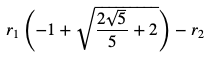裏 RjpWiki

算額（その1044）

八十七 室根村矢越 矢越弥栄神社 昭和4年(1929)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

外円の中に甲円 2 個，乙円 4 個，丙円 2 個を容れる。甲円の直径が 4 寸のとき，乙円の直径はいかほどか。

外円の半径と中心座標を R, (0, 0)
甲円の半径と中心座標を r1, (0, R - r1)
乙円の半径と中心座標を r2, (x2, r2)
丙円の半径と中心座標を r3, (0, R - r3)
とおき，以下の連立方程式を立てる。

甲円の半径 r1 は与えられるので，未知数は R, r2, x2, r3 の 4 個であるのに，条件式は 3 本しかない。条件不足かとずいぶん悩んだが，r1 と r2 の関係を求めよということなので「えいままよ」と r3 は未知数ではないと仮定して R, r2, x2 を求めてみる。
あれ不思議，r2 は r1/2 ということで，r3 は関与していない。つまり，r3 がどんな数でも（外円の大きさは r3 によって変化するが），常に r2 = r1/2 ということである。
すなわち，甲円の直径が 4 寸なら，乙円の直径は 2 寸である。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive, r2::positive, x2::positive, r3::positive
eq1 = 2r1 + 2r3 - 2R
eq2 = x2^2 + r2^2 - (R - r2)^2
eq3 = x2^2 + (R - r3 - r2)^2 - (r2 + r3)^2
res = solve([eq1, eq2, eq3], (R, r2, x2))[1]

   (r1 + r3, r1/2, sqrt(r3)*sqrt(r1 + r3))

function draw(r1, r3, more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (R, r2, x2) = (r1 + r3, r1/2, sqrt(r3)*sqrt(r1 + r3))
   @printf("甲円の直径が %g のとき，乙円の直径は %g である。\n", 2r1, 2r2)
   @printf("r1 = %g;  r3 = %g;  R = %g;  r2 = %g;  x2 = %g\n", r1, r3, R, r2, x2)
   string = @sprintf("甲円の直径 = %g　丙円の直径 = %g\n乙円の直径 = %g", 2r1, 2r3, 2r2)
   plot()
   circle(0, 0, R)
   circle22(0, R - r1, r1, :blue)
   circle22(0, R - r3, r3, :green)
   circle4(x2, r2, r2, :orange)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(R, 0, " R", :red, :left, :bottom, delta=delta/2)
       point(0, R, " R", :red, :left, :bottom, delta=delta/2)
       point(0, R - r1, "甲:r1,(0,R-r1)", :blue, :center, delta=-delta/2)
       point(0, R - r3, "丙:r3,(0,R-r3)", :green, :center, delta=-delta/2)
       point(x2, r2, "乙:r2\n(R-r2,0)", :orange, :center, delta=-delta/2)
       point(0, -0.75R, string, :black, :left, :vcenter, deltax=-10delta, mark=false)
   end
end;

draw(4/2, 6/2, true)

   甲円の直径が 4 のとき，乙円の直径は 2 である。
   r1 = 2;  r3 = 3;  R = 5;  r2 = 1;  x2 = 3.87298

draw(5/2, 7/2, true)

   甲円の直径が 5 のとき，乙円の直径は 2.5 である。
   r1 = 2.5;  r3 = 3.5;  R = 6;  r2 = 1.25;  x2 = 4.58258

甲円の直径と丙円の直径が同じ場合には以下のようになる。
これは「算額（その582）」https://blog.goo.ne.jp/r-de-r/e/a539541dcbea774663b1214354485621 と同じで，甲円と乙円の大きさが 2:1 になるというのは容易に導ける（条件不足にならないから，連立方程式をすんなりと解くことができるから）。

draw(5/2, 5/2, true)

   甲円の直径が 5 のとき，乙円の直径は 2.5 である。
   r1 = 2.5;  r3 = 2.5;  R = 5;  r2 = 1.25;  x2 = 3.53553

今話題の ChatGPT ですが，以前は画像内の情報を認識できなかったと思いますが，最新版ではちゃんと認識できる様になったようです。

そこで，暗算でも解ける算額（その1043）を解かせてみました。
https://blog.goo.ne.jp/r-de-r/e/1714af3a95e2261eea621101760acf59

与えた条件は r1, r2, r3 の相互関係を示す以下の図と，算額の「問」に書かれている条件，r2 - r3 = 1/2，r1 - r3 = 1  だけです。

最初は条件をうまく読み取れなかった（あるいは読み取った情報のどれを使えばよいかわからなかった）のか，無限ループに陥り（子犬が自分の尻尾を追いかけ，ぐるぐる回る状態），途中で終了。

見かねて，「図から r1 = r2 + r3 は読み取れましたか?」と聞いてみると...

以下のように，「条件を見落としていました...」という言い訳をして，正解を導いてしまいました。r1 = r2 + r3 をわたしが与えたので，ちょっとインチキ臭いですが。

算額（その1043）

八十六 室根村室根山 室根神社 明治32年(1899)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

長方形の中に大円 2 個，中円 4 個，小円 7 個を容れる。小円と中円の直径の差が 1 寸。小円と大円の直径の差が 2 寸のとき，小円の直径はいかほどか。

暗算で答えが出る。小円の直径は 1 寸である。
術は二次方程式を立てて求解している。山村もなんの批判もなくオウム返しで解説している。

仕方ない。SymPy でもやるか。
大円，中円，小円の半径を r1, r2, r3 とする。
以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms r1::positive, r2::positive, r3::positive
eq1 = r2 - r3 - 1//2
eq2 = r1 - r3 - 2//2
eq3 = r2 + r3 - r1
res = solve([eq1, eq2, eq3], (r1, r2, r3))
r1 = res[r1]
r2 = res[r2]
r3 = res[r3]
@printf("小円と中円の直径の差が 1 寸。小円と大円の直径の差が 2 寸のとき，小円の直径は %g である。\n", 2r3)

   小円と中円の直径の差が 1 寸。小円と大円の直径の差が 2 寸のとき，小円の直径は 1 である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2, r3) = (3, 2, 1) ./ 2
   (a , b) = (2r1 + r3, 2r2 + r3)
   plot([a, a, -a, -a, a], [-b, b, b, -b, -b], color=:orange, lw=0.5)
   circle4(r1 + r3, r1 + r3, r3)
   circle2(a - r3, 0, r3)
   circle(0, 0, r3)
   circle2(r1 + r3, 0, r1, :blue)
   circle2(r2 + r3, 0, r2, :green)
   circle22(0, b - r2, r2, :green)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r3, 0, " r3", :red, :left, delta=-delta)
       point(r3 + r2, 0, "r3+r2", :green, :center, delta=-delta)
       point(0, r3 + r2, " r3+r2", :green, :left, :vcenter)
       point(0, r3 + 2r2, "r3+2r2", :green, :center, :bottom, delta=delta)
       point(r3 + 2r1, 0, "r3+2r1 ", :blue, :right, delta=-delta)
       point(r3 + r1, r3 + r1, " (r3+r1,r3+r1)", :black, :left, :vcenter)
   end
end;

算額（その1042）

八十六 室根村室根山 室根神社 明治32年(1899)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

正方形を二個つなげたもの（つまり，長辺が短辺の 2 倍の長さの長方形）と菱形を描き，区分された領域に甲円，乙円を 2 個ずつと丙円を 8 個描く。甲円の直径が 3 寸のとき，乙円の径はいかほどか。

長方形の長辺を 4a，短辺を 2a
菱形の対角線の長い方と短い方の長さを 2x，2y
甲円の半径と中心座標を r1, (r1, 0)
乙円の半径と中心座標を r2, (0, a - r2)
丙円の半径と中心座標を r3, (2a - r3, a - r3)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms x::positive, y::positive, a::positive,
     r1::positive, r2::positive, r3::positive,
     z::positive
z = sqrt(x^2 + y^2)
eq1 = r1^2 + (a - r2)^2 - (r1 + r2)^2
eq2 = r3/(x - 2a - r3) - y/z
eq3 = r3/(y - a - r3) - x/z
eq4 = r1/(x - r1) - y/z
eq5 = dist2(x, 0, 0, y, 2a - r3, a - r3, r3);
# solve([eq1, eq2, eq3, eq4, eq5], (x, y, a, r2, r3))

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (x, y, a, r2, r3) = u
   return [
       r1^2 + (a - r2)^2 - (r1 + r2)^2,  # eq1
       r3/(-2*a - r3 + x) - y/sqrt(x^2 + y^2),  # eq2
       r3/(-a - r3 + y) - x/sqrt(x^2 + y^2),  # eq3
       r1/(-r1 + x) - y/sqrt(x^2 + y^2),  # eq4
       a^2*x^2 + 4*a^2*x*y + 4*a^2*y^2 - 2*a*r3*x^2 - 6*a*r3*x*y - 4*a*r3*y^2 - 2*a*x^2*y - 4*a*x*y^2 + 2*r3^2*x*y + 2*r3*x^2*y + 2*r3*x*y^2 + x^2*y^2,  # eq5
   ]
end;

r1 = 3/2
iniv = BigFloat[4.6, 2.5, 1.7, 0.5, 0.4]
res = nls(H, ini=iniv)

   ([4.607501170411728, 2.5395007022470373, 1.7062705739446646, 0.45401022845174593, 0.3890264955968368], true)

甲円の直径が 3 寸のとき，「答曰乙円径二寸」とあるが，算額の図を見るだけでそんな解はない。そんな図は描けない。
山村も，術を鸚鵡返ししているだけで，答，術がおかしいことを指摘していない。

甲円の直径が 3 のとき，乙円の直径は 0.90802 である。
その他のパラメータは以下のとおりである。
r1 = 1.5;  x = 4.6075;  y = 2.5395;  a = 1.70627;  r2 = 0.45401;  r3 = 0.389026

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r1 = 3/2
   (x, y, a, r2, r3) = [4.607501170411728, 2.5395007022470373, 1.7062705739446646, 0.45401022845174593, 0.3890264955968368]
   @printf("甲円の直径が %g のとき，乙円の直径は %g である。\n", 2r1, 2r2)
   @printf("r1 = %g;  x = %g;  y = %g;  a = %g;  r2 = %g;  r3 = %g\n", r1, x, y, a, r2, r3)
   plot([2a, 2a, -2a, -2a, 2a], [-a, a, a, -a, -a], color=:blue, lw=0.5)
   plot!([x, 0, -x, 0, x], [0, y, 0, -y, 0], color=:orange, lw=0.5)
   circle2(r1, 0, r1)
   circle22(0, a - r2, r2, :magenta)
   circle4(2a - r3, a - r3, r3, :green)
   circle22(0, a + r3, r3, :green)
   circle2(2a + r3, 0, r3, :green)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(r1, 0, "甲円:r1,(r1,0)", :red, :center, delta=-delta/2)
       point(0, a - r2, " 乙円:r2,(0,a-r2)", :black, :center, delta=-delta/2)
       point(0, a + r3, " 丙円:r3,(0,a+r3)", :black, :left, :vcenter)
       point(2a - r3, a - r3, " 丙円:r3,(2a-r3,a-r3)", :black, :right, :bottom, delta=delta/2, deltax=4delta)
       point(2a + r3, 0, " 丙円:r3,(2a+r3,0)", :black, :right, :bottom, delta=delta/2, deltax=5delta)
       point(2a, a, "(2a,a)", :blue, :right, :bottom, delta=delta/2)
       point(x, 0, " x", :orange, :left, :bottom, delta=delta/2)
       point(0, y, " y", :orange, :left, :bottom, delta=delta/2)
   end
end;

算額（その1041）

八十三 藤沢町保呂羽保呂羽山 保呂羽神社 明治26年(1893)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

直線の上に甲円，丙円，丁円が隣同士互いに接して載っている。さらに，丙円と丁円の上に乙円が載っている。乙円のてっぺんまでの高さはいかほどか。

乙円の半径がわかれば，算額1040 と同じ問題になる。

甲円の半径と中心座標を r1, (x1, r1)
乙円の半径と中心座標を r2, (x2,  y2)
丙円の半径と中心座標を r3, (0, r3)
丁円の半径と中心座標を r4, (x4, r4)
とおき，以下の連立方程式を解く。
高さは y2 + r2 である。

r1, r3, r4 が既知なので，x1 と x4 は簡単に計算できる。ちなみに，「算法助術」の公式40ではある。

include("julia-source.txt");

using SymPy
@syms r1::positive, r3::positive, x1::positive,
     r3::positive, r4::positive, x4::positive
     r2::positive, x2::positive, y2::positive,     
eq2 = (x1 - x4)^2 + (r1 - r4)^2 - (r1 + r4)^2 |> expand
eq5 = x4^2 + (r3 - r4)^2 - (r3 + r4)^2 |> expand;
res1 = solve([eq2, eq5], (x1, x4))[2]  # 2 of 2

   (2*sqrt(r1)*sqrt(r4) + 2*sqrt(r3)*sqrt(r4), 2*sqrt(r3)*sqrt(r4))

x1, x4 も既知となったので， x2, y2 も求めることができる。x4, x1 を展開するかしないかで，簡約化の程度が変わるが最終的な結果は同じである。

include("julia-source.txt");

using SymPy
@syms r1::positive, r3::positive, x1::positive,
     r3::positive, r4::positive, x4::positive,
     r2::positive, x2::positive, y2::positive
#x4 = 2sqrt(r3*r4)
#x1 = x4 + 2sqrt(r1*r4)
eq3 = x2^2 + (y2 - r3)^2 - (r2 + r3)^2 |> expand
eq4 = (x4 - x2)^2 + (y2 - r4)^2 - (r2 + r4)^2 |> expand
res2 = solve([eq3, eq4], (x2, y2))[2]  # 2 of 2

   ((2*r2*r3 - 2*r2*r4 + x4^2 + (2*r3 - 2*r4)*(x4^2*sqrt(4*r2^2 + 4*r2*r3 + 4*r2*r4 + 4*r3*r4 - x4^2)/(2*(r3^2 - 2*r3*r4 + r4^2 + x4^2)) + (-2*r2*r3^2 + 4*r2*r3*r4 - 2*r2*r4^2 + r3*x4^2 + r4*x4^2)/(2*(r3^2 - 2*r3*r4 + r4^2 + x4^2))))/(2*x4), x4^2*sqrt(4*r2^2 + 4*r2*r3 + 4*r2*r4 + 4*r3*r4 - x4^2)/(2*(r3^2 - 2*r3*r4 + r4^2 + x4^2)) + (-2*r2*r3^2 + 4*r2*r3*r4 - 2*r2*r4^2 + r3*x4^2 + r4*x4^2)/(2*(r3^2 - 2*r3*r4 + r4^2 + x4^2)))

x2, y2 を eq1 に代入し f(r2) = 0 となる方程式を抽出する（分数式の分母のみ，因数分解で0でないことが明らかな項を除く）。

eq1 = (x1 - x2)^2 + (y2 - r1)^2 - (r1 + r2)^2
eq01 = eq1(x2 => res2[1], y2 => res2[2]) |> simplify;
eq02 = numerator(eq01) |> expand |> factor 
res3 = solve(eq02.args[4], r2)[1]
res3(x1 => x4 + 2sqrt(r1*r4))(x4 => 2sqrt(r3*r4)) |> simplify |> println

   r4^2*(r1^(3/2)*sqrt(r3) + sqrt(r1)*r3^(3/2) + r1^2/4 + 3*r1*r3/2 + r3^2/4)/(2*r1^(3/2)*r3^(3/2) - r1^(3/2)*sqrt(r3)*r4 - sqrt(r1)*r3^(3/2)*r4 + r1^2*r3 + r1*r3^2 - 2*r1*r3*r4)

以上をまとめる。
注：SymPy では式の定義は，ほかの式にも引き継がれるので，最終的な式は定義したものよりも複雑になる。プログラム言語では式は即時に評価されるので，式の長さ（複雑さ）が変わることはない。

using SymPy
@syms r1::positive, r3::positive, x1::positive,
     r3::positive, r4::positive, x4::positive,
     r2::positive, x2::positive, y2::positive
   x4 = 2sqrt(r3*r4)
   x1 = x4 + 2sqrt(r1*r4)
   r2 = r4^2*(r1^(3/2)*sqrt(r3) + sqrt(r1)*r3^(3/2) + r1^2/4 + 3r1*r3/2 + r3^2/4)/(2r1^(3/2)*r3^(3/2) - r1^(3/2)*sqrt(r3)*r4 - sqrt(r1)*r3^(3/2)*r4 + r1^2*r3 + r1*r3^2 - 2r1*r3*r4)
   x2 = (2r2*r3 - 2r2*r4 + x4^2 + (2r3 - 2r4)*(x4^2*sqrt(4r2^2 + 4r2*r3 + 4r2*r4 + 4r3*r4 - x4^2)/(2(r3^2 - 2r3*r4 + r4^2 + x4^2)) + (-2r2*r3^2 + 4r2*r3*r4 - 2r2*r4^2 + r3*x4^2 + r4*x4^2)/(2(r3^2 - 2r3*r4 + r4^2 + x4^2))))/2x4
   y2 = x4^2*sqrt(4r2^2 + 4r2*r3 + 4r2*r4 + 4r3*r4 - x4^2)/(2*(r3^2 - 2r3*r4 + r4^2 + x4^2)) + (-2r2*r3^2 + 4r2*r3*r4 - 2r2*r4^2 + r3*x4^2 + r4*x4^2)/(2*(r3^2 - 2*r3*r4 + r4^2 + x4^2));

r2 はかなり長い式になり，SymPy ではうまく簡約化できないが，手作業でやると以下のようになる。

num = r4^2*(r1^(3/2)*sqrt(r3) + sqrt(r1)*r3^(3/2) + r1^2/4 + 3r1*r3/2 + r3^2/4)
den = (2r1^(3/2)*r3^(3/2) - r1^(3/2)*sqrt(r3)*r4 - sqrt(r1)*r3^(3/2)*r4 + r1^2*r3 + r1*r3^2 - 2r1*r3*r4);

@syms t1, t3
num.args[2](sqrt(r1) => t1)(sqrt(r3) => t3) |> simplify |> println

   t1^4/4 + 3*t1^2*t3^2/2 + t1*t3^3.0 + t1^3.0*t3 + t3^4/4

t1^4/4 + 3t1^2*t3^2/2 + t1*t3^3 + t1^3*t3 +t3^4/4 |> factor |> println

   (t1 + t3)^4/4

num2 = r4^2*(√r1 + √r3)^4/4
num2 |> println

   r4^2*(sqrt(r1) + sqrt(r3))^4/4

num(r1 => 5, r3 => 3, r4 => 2).evalf(), num2(r1 => 5, r3 => 3, r4 => 2).evalf()

   (247.935467078637, 247.935467078637)

den(sqrt(r1) => t1)(sqrt(r3) => t3) |> println

   -2*r4*t1^2*t3^2 - r4*t1*t3^3.0 - r4*t1^3.0*t3 + t1^4*t3^2 + t1^2*t3^4 + 2*t1^3.0*t3^3.0

den2 = -2*r4*t1^2*t3^2 - r4*t1*t3^3 - r4*t1^3*t3 + t1^4*t3^2 + t1^2*t3^4 + 2*t1^3*t3^3;
den2 |> factor |> println

   -t1*t3*(r4 - t1*t3)*(t1 + t3)^2

den2 = -√r1*√r3*(r4 - √r1*√r3)*(√r1 + √r3)^2
den2 |> println

   -sqrt(r1)*sqrt(r3)*(sqrt(r1) + sqrt(r3))^2*(-sqrt(r1)*sqrt(r3) + r4)

den(r1 => 5, r3 => 3, r4 => 2).evalf(), den2(r1 => 5, r3 => 3, r4 => 2).evalf()

   (114.221766846904, 114.221766846904)

r2 は最終的に以下のように比較的短い式で表すことができる。

r2 = num2/den2
r2 = r2 |> simplify
r2 |> println

   r4^2*(2*sqrt(r1)*sqrt(r3) + r1 + r3)/(4*(-sqrt(r1)*sqrt(r3)*r4 + r1*r3))

甲円，丙円，丁円の直径が 8, 5, 4 のとき，乙円のてっぺんまでの高さは 10.883036880224509 である。

(r1, r3, r4) = (8, 5, 4) ./ 2
x4 = 2sqrt(r3*r4)
x1 = x4 + 2sqrt(r1*r4)
r2 = r4^2*(2*sqrt(r1)*sqrt(r3) + r1 + r3)/(4*(-sqrt(r1)*sqrt(r3)*r4 + r1*r3))
x2 = (2r2*r3 - 2r2*r4 + x4^2 + (2r3 - 2r4)*(x4^2*sqrt(4r2^2 + 4r2*r3 + 4r2*r4 + 4r3*r4 - x4^2)/(2(r3^2 - 2r3*r4 + r4^2 + x4^2)) + (-2r2*r3^2 + 4r2*r3*r4 - 2r2*r4^2 + r3*x4^2 + r4*x4^2)/(2(r3^2 - 2r3*r4 + r4^2 + x4^2))))/2x4
y2 = x4^2*sqrt(4r2^2 + 4r2*r3 + 4r2*r4 + 4r3*r4 - x4^2)/(2*(r3^2 - 2r3*r4 + r4^2 + x4^2)) + (-2r2*r3^2 + 4r2*r3*r4 - 2r2*r4^2 + r3*x4^2 + r4*x4^2)/(2*(r3^2 - 2*r3*r4 + r4^2 + x4^2))
(x4, x1, r2, x2, y2) |> println
height = y2 + r2
height |> println

   (4.47213595499958, 10.12899020449196, 3.4892527130926094, 3.452828490790752, 7.393784167131899)
   10.883036880224509

術は，以下のように非常に短い式を提示している。

using SymPy
@syms d1, d3, d4  # r1, r3, r4 の 2 倍（直径）
(d1, d3, d4) = (8, 5, 4)
A = sqrt(d1*d3)
B = d4/A
C = 1 - B
高 = d4/C
高 |> println

   10.883036880224505

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r3, r4) = (8, 5, 4) ./ 2
   x4 = 2sqrt(r3*r4)
   x1 = x4 + 2sqrt(r1*r4)
   r2 = r4^2*(2*sqrt(r1)*sqrt(r3) + r1 + r3)/(4*(-sqrt(r1)*sqrt(r3)*r4 + r1*r3))
   x2 = (2r2*r3 - 2r2*r4 + x4^2 + (2r3 - 2r4)*(x4^2*sqrt(4r2^2 + 4r2*r3 + 4r2*r4 + 4r3*r4 - x4^2)/(2(r3^2 - 2r3*r4 + r4^2 + x4^2)) + (-2r2*r3^2 + 4r2*r3*r4 - 2r2*r4^2 + r3*x4^2 + r4*x4^2)/(2(r3^2 - 2r3*r4 + r4^2 + x4^2))))/2x4
   y2 = x4^2*sqrt(4r2^2 + 4r2*r3 + 4r2*r4 + 4r3*r4 - x4^2)/(2*(r3^2 - 2r3*r4 + r4^2 + x4^2)) + (-2r2*r3^2 + 4r2*r3*r4 - 2r2*r4^2 + r3*x4^2 + r4*x4^2)/(2*(r3^2 - 2*r3*r4 + r4^2 + x4^2))
   @printf("甲円，丙円，丁円の直径がそれぞれ %g, %g, %g のとき，乙円のてっぺんまでの高さは %g である。\n", 2r1, 2r3, 2r4, y2 + r2)
   @printf("r1 = %g;  x1 = %g;  r2 = %g;  x2 = %g;  y2 = %g;  r3 = %g;  r4 = %g;  x4 = %g\n", r1, x1, r2, x2, y2, r3, r4, x4)
   plot()
   circle(x1, r1, r1)
   circle(x2, y2, r2, :green)
   circle(0, r3, r3, :blue)
   circle(x4, r4, r4, :magenta)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x1, r1, "甲円:r1,(x1,r1)", :red, :center, delta=-delta)
       point(x2, y2, "乙円:r2,(x2,y2)", :green, :center, delta=-delta)
       point(0, r3, "丙円:r3,(0,r3)", :blue, :center, delta=-delta)
       point(x4, r4, "丁円:r4,(x4,r4)", :magenta, :center, delta=-delta)
       point(x2, y2 + r2, "高さ:y2+r2", :green, :center, :bottom, delta=delta)
   end
end;

算額（その1040）

八十三 藤沢町保呂羽保呂羽山 保呂羽神社 明治26年(1893)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

直線の上に甲円，乙円が互いに接して載っている。その 2 つの円の上に丙円が載っている。3 個の円の直径が与えられたとき，丙円のてっぺんまでの高さを求めよ。

甲円の半径と中心座標を r1, (x1, r1)
乙円の半径と中心座標を r2, (0, r2)
丙円の半径と中心座標を r3, (x3, y3)
とおき，以下の連立方程式を解く。
高さは y3 + r3 である。

include("julia-source.txt");

using SymPy
@syms r1::positive, x1::positive, r2::positive,
     r3::positive, x3::positive, y3
eq1 = x1^2 + (r1 - r2)^2 - (r1 + r2)^2 |> expand
eq2 = (x1 - x3)^2 + (y3 - r1)^2 - (r1 + r3)^2 |> expand
eq3 = x3^2 + (y3 - r2)^2 - (r2 + r3)^2 |> expand
#res = solve([eq1, eq2, eq3], (x1, x3, y3))[1];  # 1 of 2

SymPy で解くと，x1 の式が信じられないくらい長くなってしまうので，別途解く。
x1 = 2sqrt(r1*r2) である。ちなみに，「算法助術」の公式40ではある。

ans_x1 = solve(eq1, x1)[1]
ans_x1 |> println

   2*sqrt(r1)*sqrt(r2)

x3, y3 も別々に解いたほうが若干短くなるが，連立方程式として解く。eq2 は x1 を含むので，代入しておく。

eq2 = eq2(x1 => ans_x1);
(ans_x3, ans_y3) = solve([eq2, eq3], (x3, y3))[2];  # 2 of 2

ans_x3 = ans_x3 |> factor
ans_x3 |> println

   2*sqrt(r1)*sqrt(r2)*(r1*r2 - r1*sqrt(r3)*sqrt(r1 + r2 + r3) - r1*r3 + r2^2 + r2*sqrt(r3)*sqrt(r1 + r2 + r3) + r2*r3)/(r1 + r2)^2

ans_y3 = ans_y3 |> factor
ans_y3 |> println

   (2*r1^2*r2 - r1^2*r3 + 2*r1*r2^2 + 4*r1*r2*sqrt(r3)*sqrt(r1 + r2 + r3) + 2*r1*r2*r3 - r2^2*r3)/(r1 + r2)^2

ans_x1(r1 => 5/2, r2 => 3/2, r3 => 2/2).evalf() |> println
ans_x3(r1 => 5/2, r2 => 3/2, r3 => 2/2).evalf() |> println
ans_y3(r1 => 5/2, r2 => 3/2, r3 => 2/2).evalf() |> println

   3.87298334620742
   0.669041418324543
   3.90881372890605

高さは,ans_y3 + r3 = 3.90881372890605 + 1 = 4.9088137289060505 である。

高さだけを求めるならば，「算法助術」の公式47を適用する。

@syms h
公式47 = r1*h + r2*h - 2r1*r2 - 2sqrt(2r1*r2*r3*h)
res = solve(公式47, h)[2]
res |> println

   2*r1*r2*(r1 + r2 + 2*sqrt(r3)*sqrt(r1 + r2 + r3) + 2*r3)/(r1^2 + 2*r1*r2 + r2^2)

res(r1 => 5/2, r2 => 3/2, r3 => 2/2).evalf() |> println

   4.90881372890605

「術」も，簡約化した結果の見た目は異なるが，公式47と等価である。

@syms r1, r2, r3
天 = 2(r1 + r2 + r3)
A = sqrt(天 * 2r3)*2
B = 天 - A + 2r3
高 = 2r1*2r2/B |> simplify
高 |> println

   2*r1*r2/(r1 + r2 + 2*r3 - 2*sqrt(r3*(r1 + r2 + r3)))

高(r1 => 5/2, r2 => 3/2, r3 => 2/2).evalf() |> println

   4.90881372890605

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2, r3) = (5, 3, 2) ./ 2
   x1 = 2*sqrt(r1)*sqrt(r2)
   x3 = 2*sqrt(r1)*sqrt(r2)*(r1*r2 - r1*sqrt(r3)*sqrt(r1 + r2 + r3) - r1*r3 + r2^2 + r2*sqrt(r3)*sqrt(r1 + r2 + r3) + r2*r3)/(r1 + r2)^2
   y3 = (2*r1^2*r2 - r1^2*r3 + 2*r1*r2^2 + 4*r1*r2*sqrt(r3)*sqrt(r1 + r2 + r3) + 2*r1*r2*r3 - r2^2*r3)/(r1 + r2)^2
   @printf("甲円，乙円，丙円の直径がそれぞれ %g, %g, %g のとき，盤面から丙円のてっぺんまでの高さは %g である。\n", 2r1, 2r2, 2r3, y3 + r3)
   @printf("x1 = %g;  x3 = %g;  y3 = %g\n",x1, x3, y3)
   plot()
   circle(x1, r1, r1)
   circle(0, r2, r2, :green)
   circle(x3, y3, r3, :blue)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x1, r1, "甲円:r1,(x1,r1)", :red, :center, delta=delta)
       point(0, r2, "乙円:r2,(0,r2)", :green, :center, delta=delta)
       point(x3, y3, "丙円:r3,(x3,y3)", :blue, :center, delta=delta)
       point(x3, y3 + r3, "高さ=y3+r3", :magenta, :center, :bottom, delta=delta)
   end
end;

算額（その1039）

八十二 藤沢町保呂羽保呂羽山 保呂羽神社 明治7年(1874)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

大円の中に中円 2 個，小円 5 個を容れる。小円の直径が 1 寸のとき，中円の直径はいかほどか。

大円の半径と中心座標を R, (0, 0)
中円の半径と中心座標を 2r3, (x32, 0); x32 = x3 - 3r3 < 0
小円の半径と中心座標を r3, (x3, r3), x(3 - 3r3, 0)
とおき以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, r3::positive, x3::positive
x32 = x3 - 3r3
eq1 = x32^2 + r3^2 - (R - 2r3)^2
eq2 = x3^2 + r3^2 - (R - r3)^2;
res = solve([eq1, eq2], (R, x3))[2]  # 2 of 2

   (-3*r3 + 3*r3*(sqrt(6)/4 + 3/2), r3*(sqrt(6)/4 + 3/2))

res[1] |> simplify |>  println

   3*r3*(2 + sqrt(6))/4

大円の半径は小円の半径の 3(2 + √6)/4 倍である。
小円の直径が 1 寸のとき，大円の直径は 3.337117307087383 寸である。

その他のパラメータは以下のとおりである。
r3 = 0.5;  R = 1.66856;  x3 = 1.05619;  x32 = -0.443814

3(2 + √6)/4

   3.337117307087383

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r3 = 1/2
   (R, x3) = (-3*r3 + 3*r3*(sqrt(6)/4 + 3/2), r3*(sqrt(6)/4 + 3/2))
   x32 = x3 - 3r3
   @printf("小円の直径が %g のとき，大円の直径は %g である。\n", 2r3, 2R)
   @printf("r3 = %g;  R = %g;  x3 = %g;  x32 = %g\n", r3, R, x3, x32)
   plot()
   circle(0, 0, R)
   circle22(x32, 2r3, r3, :green)
   circle22(x32, r3, 2r3, :blue)
   circle22(x3, r3, r3, :green)
   circle(x32, 0, r3, :green)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x3, r3, "小円:r3,(x3,r3)", :green, :center, delta=-delta/2)
       point(x32, 0, "小円:r3,(x32,0)", :green, :center, delta=-delta/2)
       point(x32, r3, "中円:r2\n(x32,r3)", :blue, :center, :bottom, delta=delta)
       point(R, 0, " R", :red, :left, :bottom, delta=delta/2)
   end
end;

算額（その47）

岩手県東磐井郡藤沢町 藤勢寺 元治 2 年
http://www.wasan.jp/iwate/fujise.html

七十九 藤沢町藤沢道場 藤勢寺 元治2年
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

前者のリンクは，画像が不鮮明で，問，答，術とも正確に読めていなかった。
後者のリンク内容に基づき，第二版を作成する。

1 辺が 1 寸の正方形に2種類の円が収まっている。それぞれの径を求めよ。
注：算額の図では円が2種類あるように見えるが，問では「小円6個」と書いてある。

正方形の一辺の長さを a
小円の半径と中心座標を r, (x1, r), (r, x1), (x2, x2)
菱形の頂点座標を (x0, x0)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy

@syms a::positive, r::positive,
     x0::positive, x1::positive, x2::positive;
eq1 = dist2(a, 0, 0, a, x2, x2, r)
eq2 = dist2(a, 0, x0, x0, x2, x2, r)
eq3 = dist2(a, 0, x0, x0, x1, r, r)
eq4 = dist2(0, 0, a, a, x1, r, r)
res = solve([eq1, eq2, eq3, eq4], (r, x0, x1, x2))[6]  # 6 of 8

   (a*(-4553*sqrt(-10 + 12*sqrt(2)) - 4605*sqrt(-5 + 6*sqrt(2)) - 3537 + 17080*sqrt(2))/(2*(-4663*sqrt(-5 + 6*sqrt(2)) - 351*sqrt(2)*sqrt(-5 + 6*sqrt(2)) + 3845 + 4092*sqrt(2))), a*(-104*sqrt(2) - 3 + 25*sqrt(-10 + 12*sqrt(2)) + 45*sqrt(-5 + 6*sqrt(2)))/(12*(-6*sqrt(2) + 1 + 4*sqrt(-5 + 6*sqrt(2)))), (-4*sqrt(2)*a*sqrt(-5 + 6*sqrt(2)) - 5*a*sqrt(-5 + 6*sqrt(2)) + 5*sqrt(2)*a + 13*a)/(8 - 4*sqrt(-5 + 6*sqrt(2))), a*(-sqrt(2)/8 + 1/4 + sqrt(-5/32 + 3*sqrt(2)/16)))

a = 10
r = a*(-4553*sqrt(-10 + 12√2) - 4605*sqrt(-5 + 6√2) - 3537 + 17080√2)/(2*(-4663*sqrt(-5 + 6√2) - 351√2*sqrt(-5 + 6√2) + 3845 + 4092√2))
x0 = a*(-104√2 - 3 + 25*sqrt(-10 + 12√2) + 45*sqrt(-5 + 6√2))/(12*(-6√2 + 1 + 4*sqrt(-5 + 6√2)))
x1 = (-4√2a*sqrt(-5 + 6√2) - 5*a*sqrt(-5 + 6√2) + 5√2a + 13*a)/(8 - 4*sqrt(-5 + 6√2))
x2 = a*(-sqrt(2)/8 + 1/4 + sqrt(-5/32 + 3√2/16))
(r, x0, x1, x2)

   正方形の一辺の長さが 10 のとき，小円の直径は 2.73661 である。
   a = 10;  r = 1.36831;  x0 = 2.98964;  x1 = 3.30338;  x2 = 4.03246

r は，a の 6次式を解いて求めることができる。
山村は「術の式（の係数）に誤りがある」として，訂正の上で解を求めたが，「許容範囲内の誤差がある」と言っているが，そもそも山村が訂正した係数にも誤りがあるし，さらに言えば，係数は整数ではない。
どのような 6 次式なのか，手作業で方程式を解いてみる。
方針としては，eq1, eq2, eq4 の連立方程式から(a, r を含む） x0, x1, x2 （の式）を求めて，eq3 に代入して a, r を含む 式を求め，r について解く。 

res = solve([eq1, eq2, eq4], (x0, x1, x2))[3]  # 3 of 4

   ((a^3 - 4*a^2*(a/2 - sqrt(2)*r/2) + 2*a*r^2)/(-2*a^2 + 4*r^2), r*(1 + sqrt(2)), a/2 - sqrt(2)*r/2)

eq = eq3(x0 => res[1], x1 => res[2]) |> expand |> simplify
eq = numerator(eq)/a^2

    a^6/100 - 3*sqrt(2)*a^5*r/50 - a^5*r/25 + 3*sqrt(2)*a^4*r^2/25 + 6*a^4*r^2/25 - 2*sqrt(2)*a^3*r^3/25 - 8*sqrt(2)*a^2*r^4/25 - 11*a^2*r^4/25 + 2*sqrt(2)*a*r^5/25 + 4*a*r^5/25 + 4*r^6/25 + 4*sqrt(2)*r^6/25

a に定数を代入して eq = 0 を解けば r が求まる。
a = 10 としたとき，
38.62741699796952r^6+ 273.1370849898476r^5 -8925.483399593904r^4 -11313.70849898476r^3 +409705.6274847714r^2 -1.248528137423857e6r+ 1000000 = 0
である。係数は整数ではないので，「術」や山村のように整数係数を使用しても，正しい解は得られない。グラフを描けば，近似解すら得られないことがわかる。
SymPy でも解を得られないので，ニュートン・ラフソン法で数値解を求める。

function newton(fun, x1; delta = 1e-5, epsilon = 1e-14, maxrotation = 100)
   fun2(x) = (fun(x + delta) - fun(x)) / delta
   for i = 1:maxrotation
       x2 = x1 - fun(x1) / fun2(x1)
       if abs((x2 - x1) / x2) < epsilon
           return x2
       end
       x1 = x2
   end
   error("収束しませんでした")
end;

関数定義
fun(r) = 16*r^6 + 16*sqrt(2)*r^6 + 80*sqrt(2)*r^5 + 160*r^5 - 3200*sqrt(2)*r^4 - 4400*r^4 - 8000*sqrt(2)*r^3 + 120000*sqrt(2)*r^2 + 240000*r^2 - 600000*sqrt(2)*r - 400000*r + 1000000;

r = newton(fun , 1.368)
a = 10
x0 = a*(a^2 - 2*sqrt(2)*a*r - 2*r^2)/(2*(a^2 - 2*r^2))
x1 = r*(1 + sqrt(2))
x2 = a/2 - sqrt(2)*r/2
(r, x0, x1, x2)

   (1.368306828856772, 2.989643583187269, 3.30338490371374, 4.032460962571516)

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   a = 10
   r = a*(-4553*sqrt(-10 + 12√2) - 4605*sqrt(-5 + 6√2) - 3537 + 17080√2)/(2*(-4663*sqrt(-5 + 6√2) - 351√2*sqrt(-5 + 6√2) + 3845 + 4092√2))
   x0 = a*(-104√2 - 3 + 25*sqrt(-10 + 12√2) + 45*sqrt(-5 + 6√2))/(12*(-6√2 + 1 + 4*sqrt(-5 + 6√2)))
   x1 = (-4√2a*sqrt(-5 + 6√2) - 5*a*sqrt(-5 + 6√2) + 5√2a + 13*a)/(8 - 4*sqrt(-5 + 6√2))
   x2 = a*(-sqrt(2)/8 + 1/4 + sqrt(-5/32 + 3√2/16))
   @printf("正方形の一辺の長さが %g のとき，小円の直径は %g である。\n", a, 2r)
   @printf("a = %g;  r = %g;  x0 = %g;  x1 = %g;  x2 = %g\n", a, r, x0, x1, x2)
   #plot([0, a, a, 0, 0], [0, 0, a, a, 0], color=:blue, lw=0.5)
   plot([0, x0, a, a - x0, 0, a, a, 0, 0, a], [a, x0, 0, a - x0, a, 0, a, a, 0, 0], color=:blue, lw=0.5)
   segment(0, 0, x0, x0, :blue)
   segment(a, a, a - x0, a - x0, :blue)
   circle(x1, r, r)
   circle(r, x1, r)
   circle(x2, x2, r)
   circle(a - x1, a - r, r)
   circle(a - r, a - x1, r)
   circle(a - x2, a - x2, r)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a, 0, " a", :blue, :left, :bottom, delta=delta/2)
       point(x0, x0, "(x0,x0)", :black, :left, :bottom, delta=delta/2)
       point(x1, r, "小円:r,(x1,r)", :red, :center, delta=-delta/2)
       point(x2, x2, "小円:r,(x2,x2)", :red, :center, delta=-delta/2)
   end
end;

算額（その1038）

七十九 藤沢町藤沢道場 藤勢寺 元治2年
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

外円の中に交差する正方形を2個入れ，区分された領域に小円を 3 個容れる。外円の直径が 10 寸のとき，正方形の一辺の長さはいかほどか。

外円の半径と中心座標を R, (0, 0)
小円の半径と中心座標を r, (0, 0), (R - r, 0)
正方形の一辺の長さを a
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, r::positive, a::positive
b = a/√Sym(2)
eq1 = dist2(0, R - 2b, b, R - b, R - r, 0, r)
eq2 = dist2(0, R - 2b, b, R - b, 0, 0, r)
res = solve([eq1, eq2], (a, r))[2]  # 2 of 3

   (-R/7 + 11*sqrt(2)*R/14, R*(-1/7 + 2*sqrt(2)/7))

正方形の一辺の長さは a = -R/7 + 11*sqrt(2)*R/14 = R(11√2 - 2)/14 である。
外円の半径が 5 寸（直径が 10）寸のとき，5(11√2 - 2)/14 = 4.841553280751445 寸である。

「答」は 4.114 寸であるが，それでは小さすぎる。図を描いてみればわかる。山村も算額の「術」をそのまま書き写しているので，答えが変である。

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   R = 10/2
   (a, r) = (-R/7 + 11*sqrt(2)*R/14, R*(-1/7 + 2*sqrt(2)/7))
   b = a/√2
   plot([0, b, 0, -b, 0], [R - 2b, R - b, R, R - b, R - 2b], color=:blue, lw=0.5)
   plot!([0, b, 0, -b, 0], -[R - 2b, R - b, R, R - b, R - 2b], color=:blue, lw=0.5)
   circle(0, 0, R, :green)
   circle2(R - r, 0, r)
   circle(0, 0, r)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(b, R - b, "(a/√2,R-a/√2) ", :blue, :right, :vcenter)
       point(0, R - 2b, " (0,R-2a/√2)", :blue, :left, :vcenter)
       point(R - r, 0, "小円:r,(R-r,0)", :red, :center, delta=-delta/2)
       point(0, R, " R", :green, :left, :bottom, delta=delta/2)
       point(R, 0, " R", :green, :left, :bottom, delta=delta/2)
   end
end;

算額（その1037）

七十八 藤沢町藤沢早道 竹駒神社 元治2年(1865)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

直線の上に甲円，乙円，丙円が載っている。甲円，乙円の直径がそれぞれ 1 寸，2 寸のとき，丙円の直径はいかほどか。

甲円の半径と中心座標を r1, (r1, r1), (-r1, r1), (-3r1, r1)
乙円の半径と中心座標を r2, (0, y2)
丙円の半径と中心座標を r3, (-r1, y3)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms r1::positive, r2::positive, y2::positive,
     r3::positive, y3::positive
eq1 = r1^2 + (y2 - r1)^2 - (r1 + r2)^2
eq2 = 4r1^2 + (y2 - y3)^2 - (r2 + r3)^2
eq3 = r1^2 + (y3 - r1)^2 - (r1 + r3)^2
res = solve([eq1, eq2, eq3], (r3, y3, y2))[4] ## 4 of 4

   ((-2*r1^3 + 5*r1^2*r2 - r1*r2^2 - 2*r2^3 + 2*r2*sqrt(4*r1^4 - 4*r1^3*r2 - 3*r1^2*r2^2 + 2*r1*r2^3 + r2^4))/(r1^2 - 5*r1*r2 + 4*r2^2), (r1^2 - r1*sqrt(r2)*sqrt(2*r1 + r2) - 4*r1*r2 - 2*r2^(3/2)*sqrt(2*r1 + r2) + 2*sqrt(r2)*sqrt(2*r1^3 - 3*r1^2*r2 + r2^3))/(r1 - 4*r2), r1 + sqrt(r2)*sqrt(2*r1 + r2))

1.　手動による簡約化

丙円の半径 r3 は SymPy では簡約化できていないので，手作業で簡約化する。
方針としては，分子と分母を別々に簡約化（因数分解）して，結果を割り算する。

r3 = res[1]

まず，分子について検討する。平方根内の数式を因数分解する。

4*r1^4 - 4*r1^3*r2 - 3*r1^2*r2^2 + 2*r1*r2^3 + r2^4 |> factor |>println

   (r1 - r2)^2*(2*r1 + r2)^2

平方根内は二乗項の積であるが， r1 < r2 のため，ルートを外したときの符号が変わることに注意する。
因数分解をして，結果として -r1*(r1 - r2)*(2*r1 + r2) になる。

num = (-2*r1^3 + 5*r1^2*r2 - r1*r2^2 - 2*r2^3 - 2*r2*(r1 - r2)*(2*r1 + r2)) |> factor

  -r1*(r1 - r2)*(2*r1 + r2)

次に，分母を因数分解する。
結果として，(r1 - 4*r2)*(r1 - r2) になる。

den = denominator(r3)|> factor

  (r1 - 4*r2)*(r1 - r2)

「分子/分母」を計算すると，約分できるb場合には自動的に約分される。
結果として -r1*(2*r1 + r2)/(r1 - 4*r2) を得る。
これは，当然であるが，術で述べられたものと同じである。

(num/den) |> println

   -r1*(2*r1 + r2)/(r1 - 4*r2)

甲円，乙円の直径がそれぞれ 1，2 のとき，丙円の直径は 0.571429 である。

その他のパラメータは以下のとおりである。
   r1 = 0.5;  r2 = 1;  y2 = 1.91421;  r3 = 0.285714;  y3 = 1.10609

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2) = (1, 2) ./ 2
   (r3, y3, y2) = ((-2*r1^3 + 5*r1^2*r2 - r1*r2^2 - 2*r2^3 + 2*r2*sqrt(4*r1^4 - 4*r1^3*r2 - 3*r1^2*r2^2 + 2*r1*r2^3 + r2^4))/(r1^2 - 5*r1*r2 + 4*r2^2), (r1^2 - r1*sqrt(r2)*sqrt(2*r1 + r2) - 4*r1*r2 - 2*r2^(3/2)*sqrt(2*r1 + r2) + 2*sqrt(r2)*sqrt(2*r1^3 - 3*r1^2*r2 + r2^3))/(r1 - 4*r2), r1 + sqrt(r2)*sqrt(2*r1 + r2))
   @printf("甲円，乙円の直径がそれぞれ %g，%g のとき，丙円の直径は %g である。\n", 2r1, 2r2, 2r3)
   @printf("その他のパラメータは以下のとおりである。\nr1 = %g;  r2 = %g;  y2 = %g;  r3 = %g;  y3 = %g\n", r1, r2, y2, r3, y3)
   plot()
   circle2(r1, r1, r1)
   circle(-3r1, r1, r1)
   circle(0, y2, r2, :green)
   circle(-2r1, y3, r3, :blue)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(-3r1, r1, "甲円:r1,(-3r1,r1)", :red, :center, delta=-delta/2)
       point(-r1, r1, "甲円:r1,(-r1,r1)", :red, :center, delta=-delta/2)
       point(r1, r1, "甲円:r1,(r1,r1)", :red, :center, delta=-delta/2)
       point(0, y2, "乙円:r2,(0,y2)", :green, :center, delta=-delta/2)
       point(-2r1, y3, "丙円:r3\n(-2r1,y3)", :blue, :center, delta=-delta/2)
   end
end;

算額（その1036）

七十三 川崎村門崎字千手堂 伊吹神社 明治17年(1884)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

外円の中に水平な弦を引き，弦の上下に大円，中円，小円を容れる。小円の直径が既知のとき，大円の直径を求めよ。

外円の半径と中心座標を R, (0, 0)
大円の半径と中心座標を r1, (0, R - r1)
中円の半径と中心座標を r2, (x2, 2r3 - R + r2)
小円の半径と中心座標を r3, (0, 3r3 - R), (0, r3, - R)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms R::positive, r1::positive,
     r2::positive, x2::positive, r3::positive
eq1 = r1 + 2r3 - R
eq2 = x2^2 + (r2 - r3)^2 - (r2 + r3)^2
eq3 = x2^2 + (2R - 2r3 - r1 - r2)^2 - (r1 + r2)^2
eq4 = x2^2 + (2r3 - R + r2)^2 - (R - r2)^2
res = solve([eq1, eq2, eq3, eq4], (R, r1, r2, x2))

   1-element Vector{NTuple{4, Sym{PyCall.PyObject}}}:
    (4*r3, 2*r3, 3*r3/2, sqrt(6)*r3)

大円の半径 r1 は小円の半径 r3 の 2 倍である。
小円の直径が 1 寸のとき，大円の半径は 2 寸である。

その他のパラメータは以下のとおりである。
R = 2;  r1 = 1;  r2 = 0.75;  x2 = 1.22474;  r3 = 0.5

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r3 = 1/2
   (R, r1, r2, x2) = (4*r3, 2*r3, 3*r3/2, sqrt(6)*r3)
   @printf("小円の直径が %g のとき，大円の半径は %g である。\n", 2r3, 2r1)
   @printf("その他のパラメータは以下のとおりである。\nR = %g;  r1 = %g;  r2 = %g;  x2 = %g;  r3 = %g\n", R, r1, r2, x2, r3)
   plot()
   circle(0, 0, R)
   circle(0, R - r1, r1, :blue)
   circle2(x2, 2r3 - R + r2, r2, :green)
   circle(0, r3 - R, r3, :magenta)
   circle(0, 3r3 - R, r3, :magenta)
   x = sqrt(R^2 - 4r3^2)
   segment(-x, -2r3, x, -2r3)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(0, R - r1, "大円:r1,(0,R-r1)", :blue, :center, delta=-delta/2)
       point(x2, 2r3 - R + r2, "中円:r2,(x2,2r3-R+r2)", :green, :center, delta=-delta/2)
       point(0, r3 - R, "小円:r3\n(0,r3−R)", :magenta, :center, delta=-delta/2)
       point(0, 3r3 - R, "小円:r3\n(0,3r3−R)", :magenta, :center, delta=-delta/2)
       point(0, R, " R", :red, :left, :bottom, delta=delta/2)
   end
end;

算額（その1035）

五十六 花泉町金沢沼倉 沼倉熊野神社 天保14年(1843)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

円弧の弦の上に大小の正三角形と等円を容れる。等円の直径が与えられたときに弦の長さを求めよ。

円弧がその一部である外円の半径と中心座標を R, (0, 0)
大きな正三角形，小さな正三角形の一辺の長さをそれぞれ 2a 2b
等円の半径と中心座標を r, (a, y0 + 2r)
とおき，以下の連立方程式を解く。
求める弦の長さは 2a + 4b である。

include("julia-source.txt");

using SymPy
@syms a::positive, b::positive, R::positive,
     r::positive, y0::positive, x::positive,
     y::positive
y = y0 + 2r
eq1 = y0 + √Sym(3)a - R
eq2 = (a + 2b)^2 + y0^2 - R^2
eq3 = (a + b)^2 + (y0 + √Sym(3)b)^2 - R^2
eq4 = a^2 + y^2 - (R - r)^2
res = solve([eq1, eq2, eq3, eq4], (a, b, R, y0))[1]

   (r*(sqrt(3) + sqrt(6))/2, r*(-sqrt(6) - sqrt(3))/4 + sqrt(15)*r*sqrt(2*sqrt(2) + 3)/4, 2*r*(1 + sqrt(2)), r*(1/2 + sqrt(2)/2))

弦の長さは 2a + 4b なので，以下のように簡約化すると，等円の半径の (√15 + √30) 倍である。
等円の直径が 1 寸のとき，弦の長さは (√15 + √30)/2 = 4.675104460629539 である。

2res[1] + 4res[2] |> simplify |> sympy.sqrtdenest |> factor |> println

   r*(sqrt(15) + sqrt(30))

山村は術の解説（記述）をここでも間違えている。
「置五分開平方加七分五厘一十五之開平方乗等円径」を「置五個開平方加七分五厘一十五之開平方乗等円径」と誤記している。
当然答えも間違っている。

println(sqrt((sqrt(5) + 0.75)*15), " 誤")

   6.692609331381658 誤

println(sqrt((sqrt(0.5) + 0.75)*15), " 正")

   4.675104460629539 正

0.5, 0.75 を分数として取り扱って簡約化すると以下のようにきれいな形になる。
つまり，(√15 + √30)/2 で，前述した解析解と一致する（当たり前だが）。

sqrt((sqrt(Sym(5)//10)+ 3//4)*15) |> simplify |> sympy.sqrtdenest |> factor |> println

   (sqrt(15) + sqrt(30))/2

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r = 1/2
   (a, b, R, y0) = (r*(sqrt(3) + sqrt(6))/2, r*(-sqrt(6) - sqrt(3))/4 + sqrt(15)*r*sqrt(2*sqrt(2) + 3)/4, 2*r*(1 + sqrt(2)), r*(1/2 + sqrt(2)/2))
   y = y0 + 2r
   @printf("等円の直径が %g のとき，弦の長さは %.15g である。\n", 2r, 2a + 4b)
   plot([a + 2b, -a - 2b, -a - b, -a, 0, a, a + b, a + 2b],
   y0 .+ [0, 0, √3b, 0, √3a, 0, √3b, 0], color=:green, lw=0.5)
   circle(0, 0, R, beginangle=-10, endangle=190)
   circle2(a, y, r, :blue)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(R, 0, " R", :red, :left, :bottom, delta=delta/2)
       point(0, y0, " y0", :green, :left, delta=-delta/2)
       point(a, y0, " (a,y0)", :green, :center, delta=-delta/2)
       point(a+2b, y0, "(a+2b,y0)", :green, :right, delta=-delta/2)
       point(0, y0 + √3a, " (0,y0+√3a)", :red, :center, :bottom, delta=delta/2)
       point(a + b, y0 + √3b, "(a+b,y0+√3b)", :red, :left, :bottom, delta=delta/2)
       point(a, y0+2r, "等円:r\n(a,y0+2r)", :blue, :center, delta=-delta/2)
       plot!(xlims=(-R - 2delta, R+6delta))
   end
end;

算額（その1034）

五十五 花泉町老松 林観世音堂 文政7年(1824)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

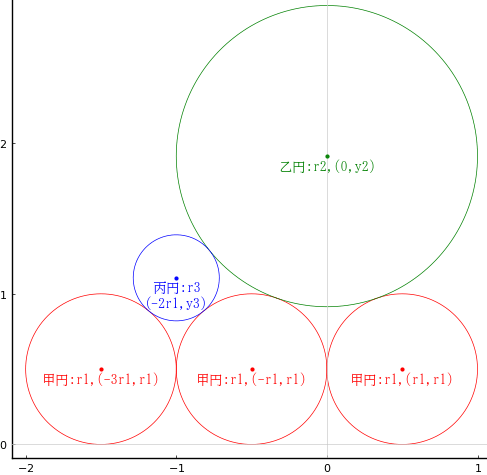
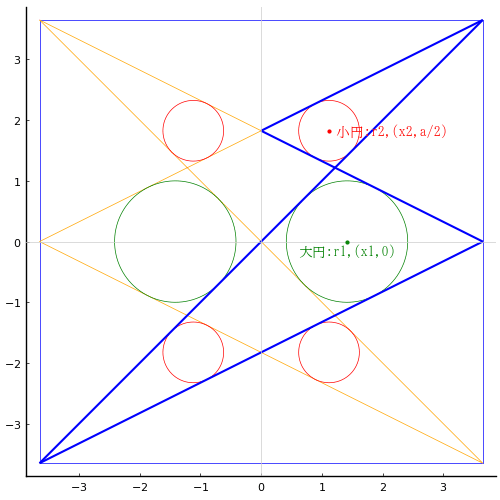
正方形の中に二等辺三角形と大円，中円，小円，甲円，乙円，丙円を容れる。小円の直径が 1 寸のとき，丙円の直径はいかほどか。

正方形の一辺の長さを 2a
大円の半径と中心座標を r1, (0, r1)
中円の半径と中心座標を r2, (0, 2r1 + r2
小円の半径と中心座標を r3, (0, 2r1 + 2r2 + r3)
甲円の半径と中心座標を r4, (a - r4, 2a - r4)
乙円の半径と中心座標を r5, (a - r5, y5)
丙円の半径と中心座標を r6, (a - r6, y6)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms a::positive, r1::positive, r2::positive,
     r3::positive, r4::positive, r5::positive,
     y5::positive, r6::positive, y6::positive
eq1 = r1/(2a - r1) - 1/√Sym(5)
eq2 = r2/(2a - 2r1 - r2) - 1/√Sym(5)
eq3 = r3/(2a - 2r1 - 2r2 - r3) - 1/√Sym(5)

# eq4 = dist2(0, 2a, a, 0, a - r4, 2a - r4, r4)
# eq5 = dist2(0, 2a, a, 0, a - r5, y5, r5)
# eq6 = dist2(0, 2a, a, 0, a - r6, y6, r6)
eq4 = a + 2a - sqrt(a^2 + 4a^2) - 2r4
eq5 = r5/y5 - r6/y6
eq6 = r4/(2a - r4) - r6/y6

eq7 = (r4 - r5)^2 + (2a - r4 - y5)^2 - (r4 + r5)^2 |> expand
eq8 = (r5 - r6)^2 + (y5 - y6)^2 - (r5 + r6)^2 |> expand
# solve([eq1, eq2, eq3, eq4, eq5, eq6, eq7, eq8],
#    (a, r1, r2, r4, r5, y5, r6, y6))

1.　a, r1, r2 を求めるのは簡単である

連立方程式は相互に独立なものが混ざっているので，逐次解いてゆくのが良策である。
正方形の一辺，二等辺三角形内の大円，中円，小円の半径を求めるためには eq1, eq2, eq3 の連立方程式を解けばよい。a, r1, r2 は与えられた r3 の関数（倍数）で表現される。

res1 = solve([eq1, eq2, eq3], (r1, r2, a))
#= a  =# res1[a] |> println

   r3*(11 + 5*sqrt(5))/2

#= r1 =# res1[r1] |> println

   r3*(3*sqrt(5) + 7)/2

#= r2 =# res1[r2] |> println

   r3*(sqrt(5) + 3)/2

2.　r4 は有名な「直角三角形に内接する円の直径」で求める

eq4 により，これも r3 の関数（倍数）で表現できる。式中に出ている a は前段階で求められているので，その定義を使う。

@syms a::positive, r1::positive, r2::positive,
     r3::positive, r4::positive, r5::positive,
     y5::positive, r6::positive, y6::positive
a = r3*(11 + 5*sqrt(Sym(5)))/2
eq4 = a + 2a - sqrt(a^2 + 4a^2) - 2r4
ans_r4 = solve(eq4, r4)[1] |> simplify
ans_r4 |> println

   r3*(2 + sqrt(5))

3.　r5, y5, r6, y6 を求める

eq5, eq6, eq7, eq8 の 4 元連立方程式を解くこともできるが，SymPy では結果の式が複雑になり簡約化もできないので，これらも逐次解くようにする。

using SymPy
@syms a::positive, r1::positive, r2::positive,
     r3::positive, r4::positive, r5::positive,
     y5::positive, r6::positive, y6::positive
r4 = r3*(2 + sqrt(Sym(5)))
eq5 = r5/y5 - r6/y6
eq6 = r4/(2a - r4) - r6/y6
eq7 = (r4 - r5)^2 + (2a - r4 - y5)^2 - (r4 + r5)^2 |> expand
eq8 = (r5 - r6)^2 + (y5 - y6)^2 - (r5 + r6)^2 |> expand;

3.1.　y5, y6 を求める

eq5, eq6 を解いて y5, y6 を求める。解の式には a, r4, r5, r6 が含まれる。a, r4 は前段階までで求められているが，r5, r6 はまだ未知数である。

res2 = solve([eq5, eq6], (y5, y6))
#= y5 =# ans_y5 = res2[y5]
ans_y5 |> println

   r5*(2*a - r4)/r4

#= y6 =# ans_y6 = res2[y6]
ans_y6 |> println

   r6*(2*a - r4)/r4

3.2.　r5, r6 を求める

前段階で求められた y5, y6 を eq7 に代入すると，これまでに求められている a, r4, 未知数 r5 の式になるので，r5 を求めることができる。

eq7 = eq7(y5 => ans_y5, y6 => ans_y6) |> simplify
eq7 |> println

   4*a^2 - 8*a^2*r5/r4 - 4*a*r4 + 8*a*r5 + r4^2 - 6*r4*r5 + r5^2*(2*a - r4)^2/r4^2

ans_r5 = solve(eq7, r5)[1]  # 1 of 2
ans_r5 |> println

   r4*(4*a^2 - 4*a*r4 + 3*r4^2 - 2*r4*sqrt(4*a^2 - 4*a*r4 + 2*r4^2))/(4*a^2 - 4*a*r4 + r4^2)

同様に，前段階で求められた y5, y6 を eq8 に代入すると，これまでに求められている a, r4, r5, 未知数 r6 の式になるので，r6 を求めることができる。

eq8 = eq8(y5 => ans_y5, y6 => ans_y6) |> simplify
eq8 |> println

   (-4*r4^2*r5*r6 + r5^2*(2*a - r4)^2 - 2*r5*r6*(2*a - r4)^2 + r6^2*(2*a - r4)^2)/r4^2

ans_r6 = solve(eq8, r6)[1]  # 1 of 2
ans_r6 |> println

   r5*(4*a^2 - 4*a*r4 + 3*r4^2 - 2*r4*sqrt(4*a^2 - 4*a*r4 + 2*r4^2))/(4*a^2 - 4*a*r4 + r4^2)

4.　連立方程式の解のまとめ

順次求めた結果をまとめると以下のようになる。
r3 は与えられた既知の数である。
r5 と r6，y5 と y6 を見ればわかるが，甲円，乙円，丙円，... の累円の半径，中心の y 座標は，前の円の定数倍になっている（等比級数である）。

@syms r3
s5 = √Sym(5)
r1 = r3*(3s5 + 7)/2
r2 = r3*(s5 + 3)/2
a = r3*(11 + 5s5)/2
r4 = a*(3 - s5)/2
r5 = r4*(4a^2 - 4a*r4 + 3r4^2 - 2r4*sqrt(4a^2 - 4a*r4 + 2r4^2))/(4a^2 - 4a*r4 + r4^2)
r6 = r5*(4a^2 - 4a*r4 + 3r4^2 - 2r4*sqrt(4a^2 - 4a*r4 + 2r4^2))/(4a^2 - 4a*r4 + r4^2)
y5 = r5*(2a - r4)/r4
y6 = r6*(2a - r4)/r4;

r6 はこの段階では非常に複雑な長い式になっている。

r6 |> display

SymPy により，r6 は以下のように簡約化できるが，後述の「術」による式は見た目は簡潔である。

r6 |> simplify |> (x -> x(sqrt(r3^2) => r3)) |> simplify |> println

   r3*(-318 - 54*sqrt(25 - 5*sqrt(5)) + 118*sqrt(5 - sqrt(5)) + 145*sqrt(5))

(-318 - 54*sqrt(25 - 5*sqrt(5)) + 118*sqrt(5 - sqrt(5)) + 145*sqrt(5))

   1.6618327599278473

丙円の直径は，小円の直径の 1.6618327599278473 倍である。

5.　数値解

単に数値解を求めるだけであれば，nlsolve() を用いて以下のようにすればよい。

using NLsolve

function nls(func, params...; ini = [0.0])
   if typeof(ini) <: Number
       r = nlsolve((vout, vin) -> vout[1] = func(vin[1], params..., [ini]), ftol=big"1e-40")
       v = r.zero[1]
   else
       r = nlsolve((vout, vin)->vout .= func(vin, params...), ini, ftol=big"1e-40")
       v = r.zero
   end
   return Float64.(v), r.f_converged
end;

function H(u)
   (a, r1, r2, r4, r5, y5, r6, y6) = u
   return [
       r1/(2*a - r1) - sqrt(5)/5,  # eq1
       r2/(2*a - 2*r1 - r2) - sqrt(5)/5,  # eq2
       r3/(2*a - 2*r1 - 2*r2 - r3) - sqrt(5)/5,  # eq3
       -sqrt(5)*a + 3*a - 2*r4,  # eq4
       r5/y5 - r6/y6,  # eq5
       r4/(2*a - r4) - r6/y6,  # eq6
       (r4 - r5)^2 - (r4 + r5)^2 + (2*a - r4 - y5)^2,  # eq7
       (r5 - r6)^2 - (r5 + r6)^2 + (y5 - y6)^2,  # eq8
   ]
end;
r3 = 1/2
iniv = BigFloat[5.5, 3.4, 1.3, 2.1, 1.3, 5.6, 0.8, 3.5]
res = nls(H, ini=iniv)

   ([5.545084971874738, 3.4270509831248432, 1.3090169943749477, 2.118033988749895, 1.326615669503669, 5.619634156033938, 0.83091637996395, 3.519818269145337], true)

6.　「術」による計算

術は，丙円の径を求める短い式を提示している。
山村の解説ではここでも，A^4 とすべきところを 4^4 と誤記している（結果は正しいが）。

@syms 小円径
天 = s5 + 2
A = (sqrt(天^2 + 1) - 1)/天
丙円径 = A^4*天*小円径

当然ながら，答えは前に示した解析解，数値解と一致する。

丙円径(小円径 => 1).evalf() |> println

   1.66183275992790

この式を SymPy で簡約化すると以下のようになる。
得られる式は，前述した解析解の簡約化された数式と同じくらいの複雑さになる。

@syms d
丙円径 = apart(丙円径, d) |> simplify |> factor |> simplify
丙円径 |> println

   小円径*(-140*sqrt(20*sqrt(5) + 50) - 318 + 145*sqrt(5) + 312*sqrt(4*sqrt(5) + 10))

(-140*sqrt(20*sqrt(5) + 50) - 318 + 145*sqrt(5) + 312*sqrt(4*sqrt(5) + 10)) |> println

   1.6618327599280747

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r3 = 1/2
   # (a, r1, r2, r4, r5, y5, r6, y6) = [5.545084971874738, 3.4270509831248432, 1.3090169943749477, 2.118033988749895, 1.326615669503669, 5.619634156033938, 0.83091637996395, 3.519818269145337]
   r1 = r3*(3√5 + 7)/2
   r2 = r3*(√5 + 3)/2
   a = r3*(11 + 5√5)/2
   r4 = a*(3 - √5)/2
   r5 = r4*(4a^2 - 4a*r4 + 3r4^2 - 2r4*sqrt(4a^2 - 4a*r4 + 2r4^2))/(4a^2 - 4a*r4 + r4^2)
   r6 = r5*(4a^2 - 4a*r4 + 3r4^2 - 2r4*sqrt(4a^2 - 4a*r4 + 2r4^2))/(4a^2 - 4a*r4 + r4^2)
   y5 = r5*(2a - r4)/r4
   y6 = r6*(2a - r4)/r4
   @printf("小円の直径が %g のとき，丙円の直径は %g である。\n", 2r3, 2r6)
   plot([a, a, -a, -a, a], [0, 2a, 2a, 0, 0], color=:blue, lw=0.5)
   plot!([-a, 0, a], [0, 2a, 0], color=:orange, lw=0.5)
   circle(0, r1, r1)
   circle(0, 2r1 + r2, r2, :green)
   circle(0, 2r1 + 2r2 + r3, r3, :blue)
   circle(a - r4, 2a - r4, r4, :magenta)
   circle(a - r5, y5, r5, :brown)
   circle(a - r6, y6, r6, :purple)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(a - r4, 2a - r4, "(a-r4,2a-r4)")
       #point(a - r5, y5, "(a-r5,y5)")
       #point(a - r6, y6, "(a-r6,y6)")
   end
end;

算額（その1033）

五十四 一関市市野々自鏡山 吾勝神社 天保6年(1835)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

正方形内に斜線を引き，区画された領域に大円と小円を容れる。小円の直径が 1 寸のとき，大円の直径はいかほどか。

計算しなくてもわかる。
斜線がたくさんあるので惑わされるが，必要なものだけ残すと，大円と小円を含む三角形は相似で，相似比が 2:1 である。よって，大円の直径は小円の直径の 2 倍である。

正方形の一辺の長さを 2a
大円の半径と中心座標を r1, (x1, 0)
小円の半径と中心座標を r2, (x2, a/2)
とおき，以下の連立方程式を解く。

include("julia-source.txt");

using SymPy
@syms a::positive, r1::positive, x1::positive,
     r2::positive, x2::positive
eq1 = dist2(-a, -a, a, a, x1, 0, r1)
eq2 = dist2(-a, -a, a, a, x2, a/2, r2)
eq3 = dist2(-a, a, a, 0, x1, 0, r1)
eq4 = dist2(-a, a, a, 0, x2, a/2, r2)
solve([eq1, eq2, eq3, eq4], (a, r1, x1, x2))[2]  # 2 of 2

   (2*r2*(sqrt(2) + sqrt(5)), 2*r2, 2*sqrt(2)*r2, sqrt(5)*r2)

小円の直径が 1 寸のとき，大円の直径は 2 寸，正方形の一辺の長さは 7.3005630797457695 寸である。

その他のパラメータは以下のとおりである。

r2 = 0.5;  a = 3.65028;  r1 = 1;  x1 = 1.41421;  x2 = 1.11803

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   r2 = 1/2
   (a, r1, x1, x2) = (2*r2*(sqrt(2) + sqrt(5)), 2*r2, 2*sqrt(2)*r2, sqrt(5)*r2)
   @printf("r2 = %g;  a = %g;  r1 = %g;  x1 = %g;  x2 = %g\n", r2, a, r1, x1, x2)
   plot([a, a, -a, -a, a], [-a, a, a, -a, -a], color=:blue, lw=0.5)
   plot!([a, -a, a, -a], [a, 0, -a, a], color=:orange, lw=0.5)
   plot!(-[a, -a, a, -a], [a, 0, -a, a], color=:orange, lw=0.5)
   circle4(x2, a/2, r2)
   circle2(x1, 0, r1, :green)
   segment(a, a, -a, -a, :blue, lw=1.5)
   segment(a, 0, -a, -a, :blue, lw=1.5)
   segment(0, a/2, a, 0, :blue, lw=1.5)
   segment(0, a/2, a, a, :blue, lw=1.5)
   if more        
       delta = (fontheight = (ylims()[2]- ylims()[1]) / 500 * 10 * 2) /3  # size[2] * fontsize * 2
       hline!([0], color=:gray80, lw=0.5)
       vline!([0], color=:gray80, lw=0.5)
       point(x1, 0, "大円:r1,(x1,0)", :green, :center, delta=-delta/2)
       point(x2, a/2, " 小円:r2,(x2,a/2)", :red, :left, :vcenter)
   end
end;

算額（その1032）

三十二 一関市舞川 観福寺内地蔵堂後額 明治34年(1901)
山村善夫：現存 岩手の算額，昭和52年1月30日，熊谷印刷，盛岡市.
http://www.wasan.jp/yamamura/yamamura.html

大小の円を用いて梅鉢紋を描く。大円，小円の直径が与えられたときに大円と小円の間の距離を求めよ。

注：ここで云う距離は図の緑色の太線の長さであり，大円と小円の中心間距離から大円と小円の半径の和を差し引いたものである。

大円と小円の半径を r1, r2，中心間距離 を l とおき，以下の方程式を解く。

include("julia-source.txt");

using SymPy
@syms l::positive, r1::positive, r2::positive
eq1 = l*sind(Sym(36)) - r1
res = solve(eq1, l)[1] - (r1 + r2)
res |> println
res |> display

   -r1 + 2*sqrt(2)*r1/sqrt(5 - sqrt(5)) - r2

術に出てくる「八分（0.8）」は 8/10 = 4/5 である。

b = (sqrt(sqrt(Sym(8)//Sym(10)) +2) - 1)*r1 - r2

簡約化すると以下のようになる。

b2 = b |> simplify

それぞれの式の見かけは違うが，SymPy で得られた式と同じである。
大円，小円の直径がそれぞれ 5, 2.5 のとき，大円と小円の距離は 0.503254041760200 である。

res(r1 => 2.5, r2 => 1.25).evalf() |> println
b(r1 => 2.5, r2 => 1.25).evalf() |> println
b2(r1 => 2.5, r2 => 1.25).evalf() |> println

   0.503254041760200
   0.503254041760200
   0.503254041760200

function draw(more=false)
   pyplot(size=(500, 500), grid=false, aspectratio=1, label="", fontfamily="IPAMincho")
   (r1, r2) = (2.5, 1.25)
   中心間距離 = 2√2*r1/sqrt(5 - √5)
   @printf("大円，小円の直径がそれぞれ %g, %g のとき，大円と小円の距離は %g である。\n", 2r1, 2r2, 中心間距離  - (r1 + r2))
   plot()
   for i = 0:4
       x = 中心間距離*cosd(i*72 + 18)
       y = 中心間距離*sind(i*72 + 18)
       segment(0, 0, x, y, :green, lw=5)
       circlef(x, y, r1, :pink)
       circle(x, y, r1, :red)
   end
   circlef(0, 0, r2, :yellow)
   circle(0, 0, r2, :brown)
end;